In this example, we will show how to reblock using MineLink software and its impact in the results of the final pit shell.

Case

To develop this exercise a model with regular blocks of 20mx20mx20m was considered. The mineralized ore body has a seam geometry shape of 200m width, 1000m long, and undefined depth. It is dipping at 45° in relation to the vertical axis and is located 50 metres below the surface. The mineralized zone has an ore grade of 0.7% Cu with a uniform distribution in the blocks. For the purpose of this exercise all the blocks have a density of 2.64 t/m³. The next figures show a plant view and a section view of the ore grade in the block model.

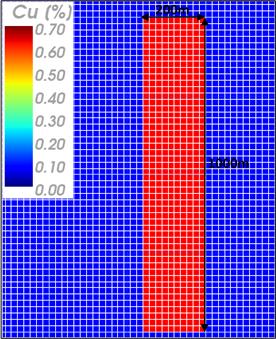Fig. 1. Plant view in the model with block dimensions of 20mx20mx20m

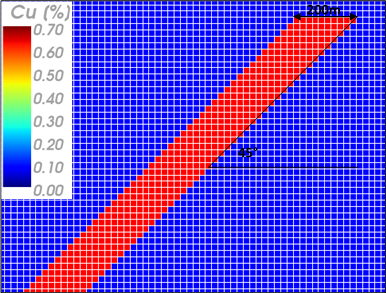Fig. 2. Section view in the model with block dimensions of 20mx20mx20m

When roblocking the original model to a block model of 40mx40mx40m, the following plant view and section view of the mineralized zone are obtained.

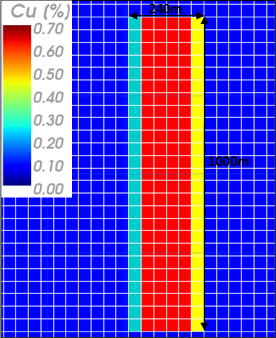Fig. 3. Plant view in the reblocked model

Fig. 4. Section view in the reblocked model

It is possible to appreciate from figures 3 and 4, when the original model is reblocked to block dimensions of 40mx40mx40m there is a dilution of the ore grade in the edges of the mineralized ore body. The next figure shows a schematic illustration of the reblocking process for a single level taking a section view.

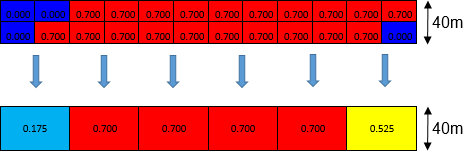Fig 5. Schematic illustration of reblocking the original block model to blocks of 40mx40mx40m

It is important to mention that figure 5 is a 2 dimension view of the reblocking process because every block of 40mx40mx40m contains 8 blocks of 20mx20mx20m.

For the optimization process a 45° overall slope angle will be considered, as well as one single metallurgical process.

The next table shows the economic parameters and the metallurgical recovery.

Table 1. Cost parameters and metallurgical recovery

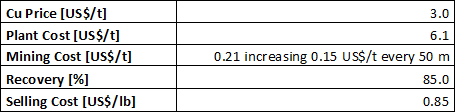Results

In this section there are some results for the reblocking and ultimate pit computation, given the block model showed in the previous section. We want to validate and compare MineLink's output given the Whittle's results using the same parameters.

Table 2. MineLink and Whittle's Ultimate Pit Results

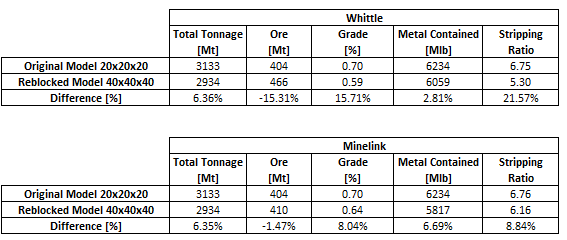On the other hand we can compare the ultimate pit shell obtained on both methodologies at the same level, as seen on next figure.

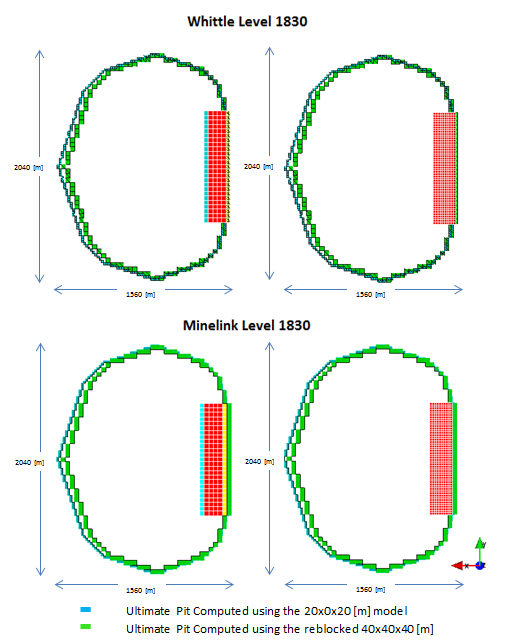Fig 6. Plan view of the ultimate pit results using the original block model (20x20x20 meters) and the reblocked model (40x40x40 meters)

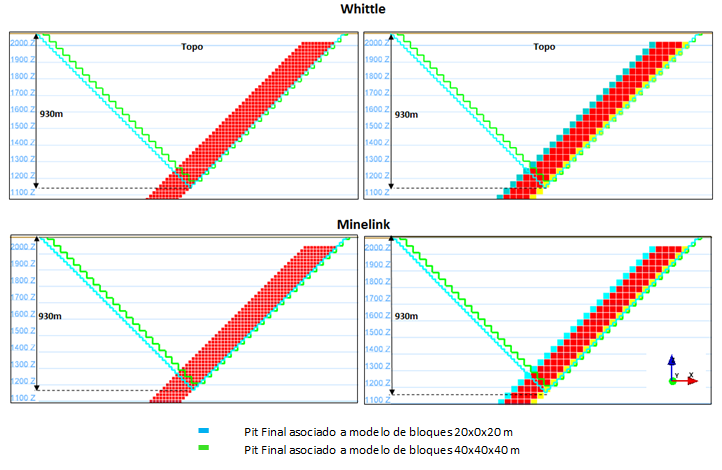Fig 7. Longitudinal view of the ultimate pit results using the original block model (20x20x20 meters) and the reblocked model (40x40x40 meters)

Reblock and Ultimate Pit MineLink’s Script

In this section is showed the script used to reblock and calculate the ultimate pit using the MineLink library.

from MineLink import *

#Import Original Block Model
bm = BlockModel(file_name = r'C:\Users\MyUser\Reblock\original_blockmodel.txt')


#________________REBLOCKING__________________________

#Reblock Dimensions
dx_reb = 40
dy_reb = 40
dz_reb = 40

#Creating a Reblocker
reg_reb = RegularReblocker(bm,dx_reb,dy_reb,dz_reb,"id")

#Add Attribute Columns to Reblocker
reg_reb.AddSummationColumn("tonnage","tonnage")
reg_reb.AddAvgColumn("density","density")
reg_reb.AddAvgColumn("grade","density","grade")
reg_reb.AddAvgColumn("recovery","density","recovery")
reg_reb.AddMaxColumn("region","region")
reg_reb.AddMaxColumn("rocktype","rocktype")

#Save the Reblocked Model
nbm = reg_reb.ReblockToRegularBlockModel()

#Export Reblocked Block Model to Text File
nbm.SaveToTextFile(r"C:\Users\MyUser\Reblock\reblocked_blockmodel.txt",["tonnage"]+["density"]+["grade"]+["recovery"]+["region"]+["rocktype"])

#______________FINAL PIT CALCULATION______________________

#Import Reblocked Block Model
bm_reb = BlockModel(file_name = r"C:\Users\MyUser\Reblock\reblocked_blockmodel.txt")

#Create Column to value attribute
bm_reb.AddColumn("value",0.0)

#ValueFunction Valorizes the Block Model Given the Attributes, Costs and Copper Price
ValueFunction(bm_reb,value,grade,rec,ton,mine_cost,proc_cost,sell_cost,price)

#Create Slope Precedences Using Rosetta
bm_reb.AddColumn("slope",45)
rosetta = RosettaSlope([360],[45])
prec = RosettaPrecedence(bm_reb,"slope")
prec.AddRosetta(45,rosetta)
prec.CreateArcs(8,dx_reb,dy_reb,dz_reb)

#Create Final Pit Instance and Calculation
names = []
fpi = FinalPitInstance("value",prec)
solver = PseudoFlowFinalPitSolver(fpi)
solver.Run()
bms = solver.FinalPit()
names.append("pit")
bms.StoreAsAttribute("pit")


#Export Reblocked Block Model Including the Pit Results
bm_reb.SaveToTextFile(r"C:\Users\MyUser\Reblock\reblocked_blockmodel_final_pit.txt",["tonnage"]+["density"]+["grade"]+["recovery"]+["region"]+["rocktype"]+["pit"])